Logic and diagrams
❖ Logical systems
Reasoning is a process that produces new information given previous data, by following
certain norms that allow us to describe inference as the unit of measurement of reasoning:
inference may be more or less (in)correct depending on the compliance or violation
of such norms.3 Logical systems, the tools used to model and better understand inference, may be
defined by pairs of the form <L,B>, where L stands for a language, and B for a semantic base (often equivalent to a calculus). Usually, some syntax is used
to determine, uniquely and recursively, the well formed expressions of the system;
while semantics is used to provide meaning to such expressions.
❖ Diagrams
In order to represent knowledge, we use internal and external representations. Internal
representations convey mental images, for example; while external representations
include physical objects on paper, blackboards, or computer screens. External representations
can be further divided into two kinds: sentential and diagrammatic (Larkin and Simon, 1987).
Sentential representations, as the name indicates, are sequences of sentences in a
particular language. Diagrammatic representations, on the other hand, are sequences
of diagrams that contain information stored at one particular locus, including information about relations with the adjacent loci; and diagrams are information graphics that index information by location on a plane
(Larkin and Simon, 1987; Nakatsu, 2010). In particular, logic diagrams are two-dimensional geometric figures with spatial relations that are isomorphic
with the structure of logical statements (Gardner, 1958: 28). The difference between diagrammatic and sentential representations is that, due
to this spatial feature, the former preserve explicitly information about topological
relations, while the latter do not-although they may, of course, preserve other kinds
of relations.
This spatial feature provides some computational advantages: diagrams group together
information avoiding large amounts of search, they automatically support a large number
of perceptual inferences, and they grant the possibility of applying operational constraints
(like free rides and overdetermined alternatives (Shimojima, 1996)) to allow the automation of perceptual inference (Larkin and Simon, 1987).
❖ Logic with diagrams
To wrap all this up, if reasoning is a process that produces new information given
previous data and information can be represented diagrammatically, it is not uncomfortable
to suggest that diagrammatic inference is the unit of measurement of diagrammatic
reasoning: diagrammatic inference would be (in)correct depending on the compliance
or violation of certain norms. Let us denote the relation of diagrammatic logical
consequence or diagrammatic inference by ►; this relation would define our intuitions
around the informal notions of visual inference or visual argument and would follow, ex hypothesi, classical structural norms (reflexivity, monotonicity, and cut), while the operator
► would follow Shimojima’s definition of a free ride as a process in which some reasoner
gains information without following any step specifically designed to gain it, i.e., a process that allows the reasoner to reach automatically (and sometimes inadvertently)
a diagrammatic representation of a conclusion from a diagrammatic representation of
premises (Shimojima, 1996: 32). VENN, as we will see in the next section, is a diagrammatic logical system of this
sort.
Syllogistic,VENN, and Non-monotonicity
The previous account of diagrammatic inference sounds reasonable, in principle; but
monotonicity does not seem to be a feasible property of diagrammatic inference due
to the spatial nature of diagrams, so to speak. In order to explain this, we will
see in what sense VENN can be used to represent some sort of (diagrammatic) non-monotonicity
and, for that, we will require a syllogistic base and a well defined diagrammatic
logical system, namely VENN.
❖ Syllogistic
Syllogistic is a term logic that has its origins in Aristotle’s Prior Analytics and is the theory of inference that deals with the consequence relation between two
categorical propositions taken as premises and another categorical proposition taken
as a conclusion. A categorical proposition is a proposition composed by two terms, a quantity, and a quality. The subject and
the predicate of a proposition are called terms: the term-schema S denotes the subject term of the proposition and the term-schema
P denotes the predicate. The quantity may be either universal (All) or particular (Some) and the quality may be either affirmative or negative. These categorical propositions are denoted
by a label, either A (universal affirmative), E (universal negative), I (particular affirmative),
or O (particular negative). A categorical syllogism, then, is a sequence of three categorical propositions ordered in such a way that
two propositions are premises and the last one is a conclusion. Within the premises
there is a term that appears in both premises but not in the conclusion. This particular
term works as a link between the remaining terms and is known as the middle term, which we denote with the term-schema M. According to this term we can set up four
figures that encode all the valid and only the valid syllogisms (Table 1).4
Table 1
Valid syllogisms
|
Figure 1
|
Figure 2
|
Figure 3
|
Figure 4
|
|
Barbara MAPSAM∴SAP
|
Cesare PAMSAM∴SAP
|
Disamis MIPMAS∴SIP
|
Calemes PAMMES∴SEP
|
|
Celarent MEPSAM∴SEP
|
Camestres PAMSEM∴SEP
|
Datisi MAPMIS∴SIP
|
Dimaris PIMMAS∴SIP
|
|
Darii MAPSIM∴SIP
|
Festino PEMSIM∴SOP
|
Bocardo MOPMAS∴SOP
|
Fresison PEMMIS∴SOP
|
|
Ferio MEPSIM∴SOP
|
Baroco PAMSOM∴SOP
|
Ferison MEPMIS∴SOP
|
|
❖ VENN
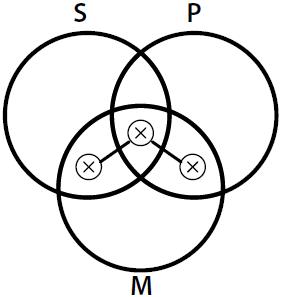
VENN is a sound and complete diagrammatic logical system (Shin, 1994) that is equivalent to monadic First Order Logic (Hammer, 1995) and thus represents syllogistic quite perspicuously. Following (Shin, 1994: 48), it has a well defined vocabulary, syntax, and semantics. Briefly, the vocabulary
is defined by the next elements: the closed curve, the rectangle, the shading, the
X, and the line (Fig. 1).
Figure 1
Syntactic elements of VENN

The semantics of VENN depends on a homomorphism with sets that helps define a diagram as any finite combination of diagrammatic elements where a region is any enclosed
area in a diagram. A basic region is a region enclosed by a rectangle or a closed curve. A minimal region is a region within which no other region is enclosed. An X sequence is a diagram of alternating X’s and lines with an X in each extremal position. Regions
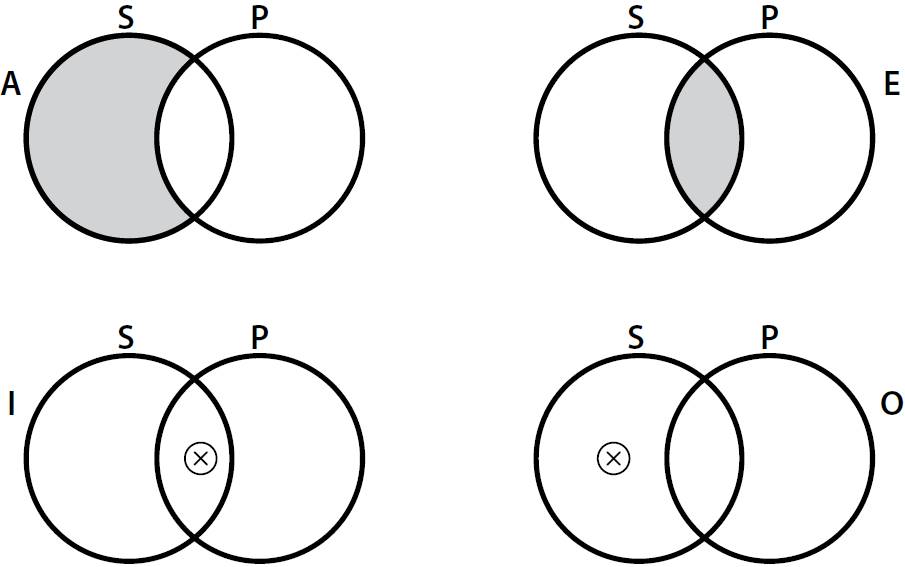
represent sets and the rectangle represents the domain. A shaded region represents an empty region and a region with an X represents a non-empty region. With these definitions, a syntax for the categorical
propositions can be elaborated (Fig. 2).
Figure.2.Categorical
propositions in VENN
The rules for this diagrammatic system are six (Shin, 1994: 81-93). (I) The rule of erasure of a diagrammatic object tells us that a well formed diagram (wfd) D
1
is obtained from a wfd D if D
1 results from either erasing a closed curve of D, or erasing a shading of some region of D, or erasing an entire X-sequence of D. (II) The rule of erasure of parts of an X-sequence says that D
1
is obtained from D if extra X-sequences have been added to some X-sequences of D. (IV) The rule of introduction of a basic region indicates that a basic region may be introduced by drawing either a rectangle or
a closed curve. (V) The rule of conflicting information says that if a diagram has a region with both a shading an X-sequence, then we may
transform the given diagram into any diagram. Finally, (VI) the rule of unification of diagrams says that D
1
is obtained from two well formed diagrams D
2
and D
3
if every region of D
1
is a counterpart region of either D
2
or D
3
and conversely. If any region of D is shaded or has an X-sequence, then it has a counterpart in either D
1
or D
2
which is also shaded or has an X- sequence and conversely.5
With these rules, VENN provides an essential feature of a well defined diagrammatic logic: a diagrammatic
method of decision (in this case, for syllogistic) that consists in drawing down the
diagrams for the premises and then checking (by mere observation) whether it is possible
to “read off” the conclusion from the drawing of the premises; in case it does, the
syllogism is valid (i.e., there is a free ride); otherwise it is invalid (i.e., there
is an overdetermined alternative).
❖ Example 1
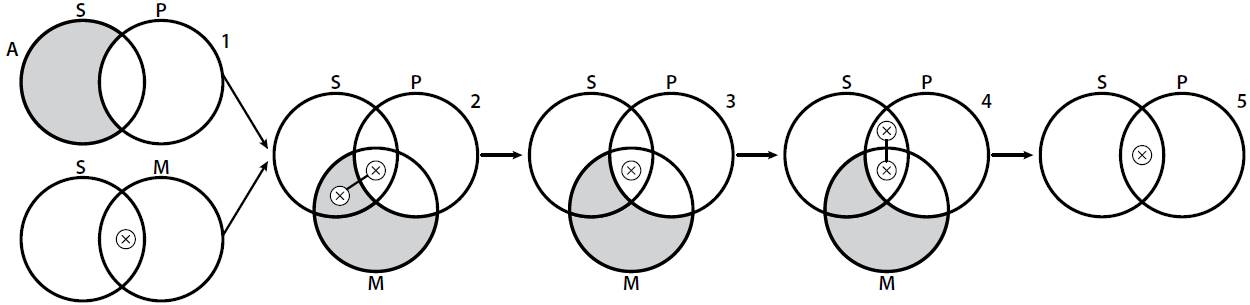
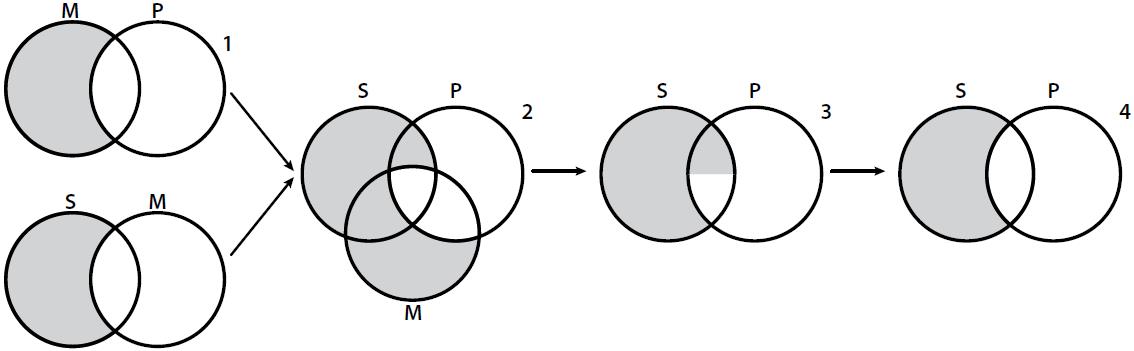
Consider a syllogism of the form MAPSIM∴SIP. According to these rules, we begin with
an introduction of areas (step 1) and then a unification is applied (step 2). After
that, we apply an erasure of an X-sequence (step 3) and then a spreading of an X-sequence
(step 4). Finally, by the erasure of a closed curve rule, we obtain a final diagram
(step 5). And since the conclusion got drawn by drawing down the premises, the diagrammatic
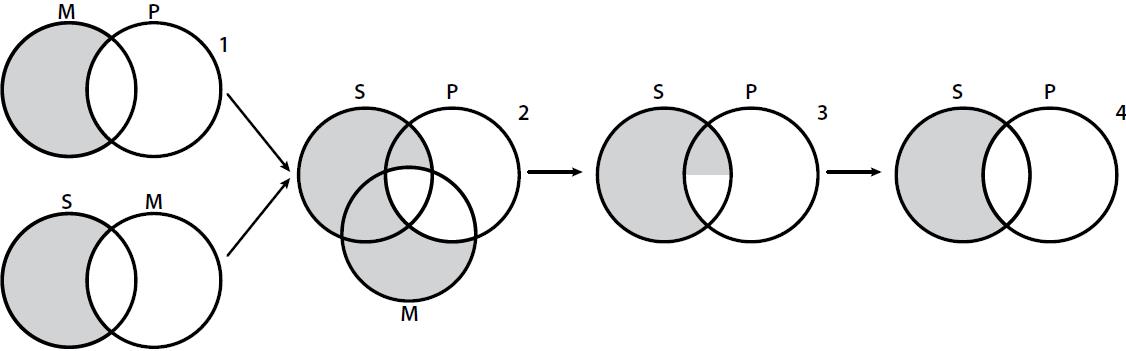
inference is valid. This is a fair example of a free ride: MAPSIM►SIP (Fig. 3).
Figure 3
An example of a free ride in VEEN
❖ Non-monotonicity with VENN
After this brief review of diagrammatic inference, we now suggest in what sense VENN provides a logical framework able to model some form of non-monotonicity. To explain
why VENN is suitable for this task, consider that non-monotonic reasoning can be characterized
by the following “equation” (Bochman, 2011):
Non-monotonic reasoning=Logic+Non-monotonic semantics.
We could say, in similar lines, that:
Non-monotonic diagrammatic reasoning=Logic+Diagrams+Nonmonotonic semantics,
or for our purposes, that:
Non-monotonic diagrammatic reasoning=Syllogistic base+VENN+ Non-monotonic semantics.
To explain in what sense we can talk about some sort of nonmonotonic semantics, let
us begin with an example in classical First Order Logic.
❖ Example 2
Consider a Barbara syllogism, i.e., a reasoning of the form MAPSAM\SAP:
-
1. ∀x(Mx→Px) MAP
-
2.∀x(Sx→Mx) SAM
-
∴∀x(Sx→Px) SAP
If we add the sentence SOP (which contains contradictory information w.r.t. the conclusion),
we can see that SAP is still a logical consequence from MAPSAMSOP:
-
1. ∀x(Mx→Px) MAP
-
2.∀x(Sx→Mx) SAM
-
3. ∃x(Sx∧¬Px) SOP
-
∴∀x(Sx→Px) SAP
But moreover, even if we follow the account of Venn given in (Shin, 1994: 81-93) we can see that, according to rule V, since from conflicting information we can
obtain any diagram, the diagram that represents SAP is still a logical consequence from the
diagram given in MAPSAMSOP, for such rule is the diagrammatic version of the “ex contradict sequitur quodlibet” rule, which not only implies some sortof monotonicity (Fig. 4), but also some sort of irrelevance (Fig. 4), but also some sort of irrelevance (Fig. 5) within VENN.
Figure 4
An example of monotonicity: MAPSAM∪SOP►SAP
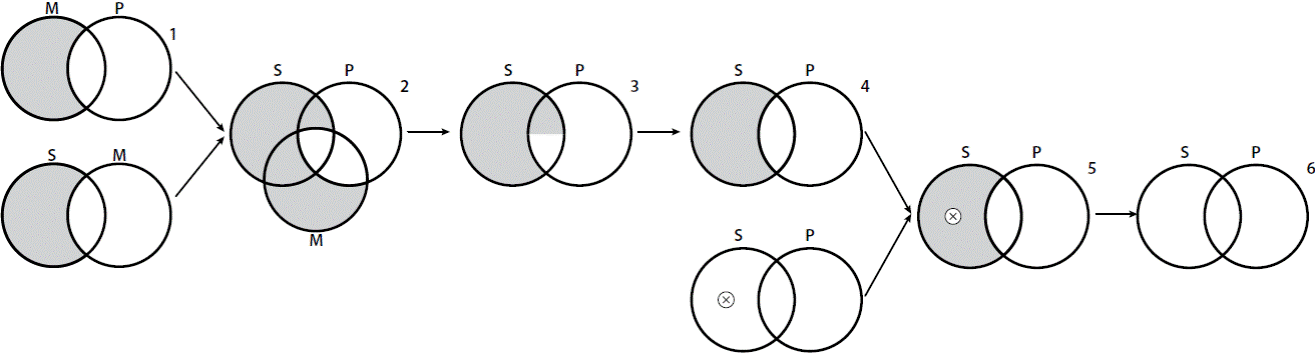
Figure 5
An example of irrelevance: MAPSAM∪SOP►SIP
However, Venn diagrams are diagrams, and so, they have spatial features and this fact has consequences. Indeed,
as Barwise and Etchemendy argue: “Diagrams are physical situations. They must be,
since we can see them. As such they obey their own set of constraints.” (Allwein et al, 1996: 23). A physical situation is a situation in the world, in this case, it is a portion
of paper (i.e. a space) on which we draw the diagrams (Shimojima, 1996: 38). Hence, the constraints Barwise and Etchemendy talk about must be spatial constraints
that should (dis)allow certain rules to work; in particular, the rule of conflicting
information should be unlikely to work properly because contradictory diagrams cannot
exist in the exact same portion of paper (i.e. the same space), because they are opposite
physical situations.
To further clarify this last point, we can refer to (Shin, 1994: 167-168). Shin argues, rather convincingly, that contradictory information can be represented
more perceptually in diagrammatic representations than in linguistic representations,
since in diagrammatic representations this kind of information becomes visually noticeable,
for conflicting spatial arrangements are evident. And to illustrate this, Shin advances
a couple of examples that we are going to reproduce. For the first one, consider the
following statements:
-
Susan is to the left of Tom.
-
Tom is to the left of Mary.
-
Mary is to the left of Susan.
In First Order Logic, these statements can be represented via the conjunction Lst∧Ltm∧Lms.
This conjunction can be shown to be a contradiction by noticing that the relation
“being left of” (denoted by Lxy) is transitive and asymmetric. But, Shin continues, although such contradiction is
not obviously revealed by the notation, it is perceptually evident with the next diagram:
The diagram above violates the following spatial constraint of this representation:
that no diagram occupies more than one place simultaneously.
As for the second example, consider the case of a timetable, which is a diagrammatic
representation of a schedule. Suppose further that we want to add a new appointment
to the timetable. If this new appointment conflicts with any existing appointments,
this conflict will be revealed clearly, since the new addition would violate the following
spatial constraint of this representation: that no space can be occupied by more than
one diagram.
What these particular examples show is that, when it comes to opposite physical situations,
we must consider two physical constraints: that no diagrammatic object occupies more
than one place simultaneously and that no space can be occupied by more than one diagrammatic
object. And these remarks give us plausible reasons to warrant some sort of non-monotonicity
within VENN, provided we interpret diagrams as legitimate inference bearers with physical properties
and not just as mediums that represent information. So, let us consider a couple of
definitions that presuppose the general notion of a physical situation.
❖ Definition 1
(Diagrammatic configuration) Let ∆={δ1,...,δn} be a sequence of diagrams for categorical propositions in VENN, let StP be any categorical proposition in syllogistic with label t∈{A, E, I, O},
and let h be a homomorphism from VENN to syllogistic s.t. h(δ)=StP. A diagrammatic configuration is Cfg(δ)={h(δ)|δ∈∆}.
❖ Definition 2
(Free ride) Let δ be a diagram for a categorical proposition in VENN and let ∆ be a finite sequence of diagrams for categorical propositions in VENN, we say δ is a free ride from ∆, ∆►δ, if and only if δ=∆ or there is a sequence of
applications of rules I-VI that allows us to transform ∆ into δ.
Now, provided we interpret diagrams as physical situations, we can account for the
next statement:
❖ Proposition 1
(Non-monotonicity) VENN allows non-monotonicity.
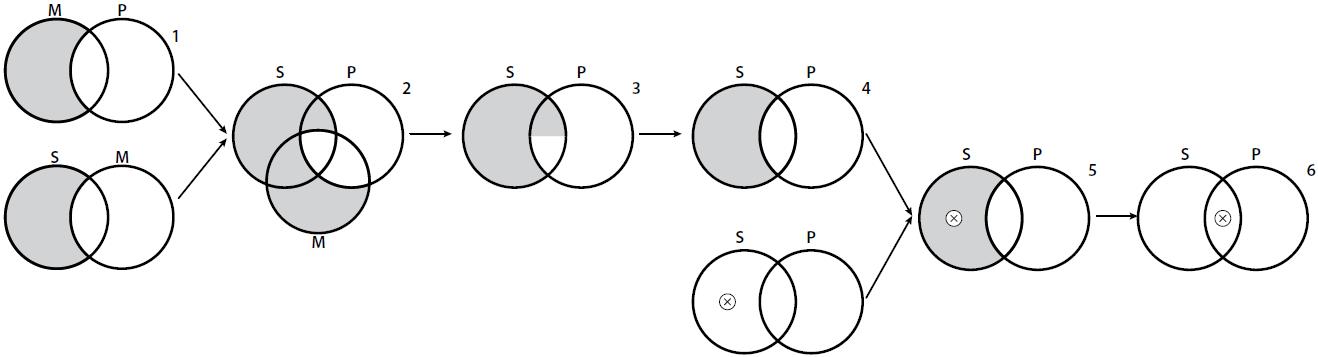
Proof. We prove this by producing a counter-example. Suppose VENN allows monotonic inference and let Cfg(∆)=MAPSAM. From such configuration we can get a free ride to the configuration Cfg(δ)=SAP, i.e., ∆►δ, as in Figure 6.
Figure 6
MAPSAM►SAP
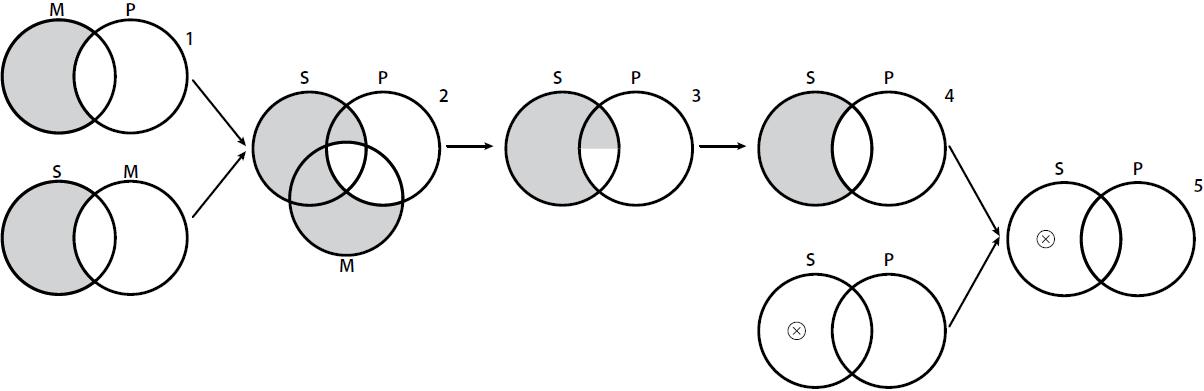
Now, as we did in Example 2, pick a contradictory diagram δ’=¬δ, i.e. pick Cfg(δ’)=SOP, and add it by an addition rule (namely, introduction of a region). Since δ and δ’ are opposite physical situations, they cannot occupy more than one
place simultaneously and no space can be occupied by the two of them, so the addition
of δ’ implies the erasure of δ by an erasure rule (namely, erasure of a diagrammatic object). This avoids any application of rule V, i.e., it disallows any combination of contradictory
diagrams, and hence, while ∆►δ holds, ∆∪{δ’}►δ does not (Fig. 7).6
Figure 7
MAPSAM∪SOP►SAP does not hold.
We can extract two consequences from this result. First, that VENN provides a logical framework able to model some form of non-monotonic diagrammatic
inference, provided diagrams are rightly interpreted as physical situations.7 And second, that we can advance the idea of non-monotonic diagrammatic systems that
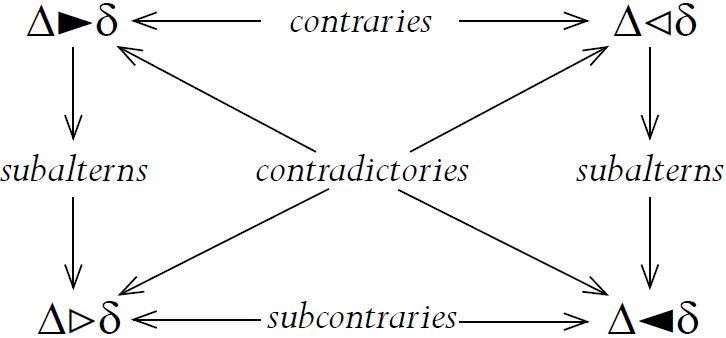
we could approximate, for example, with rules à la Nute (2003), by letting > denote a preference relation over diagrams, ► denote a strong free ride, ⊳ a weak free ride, and ◄ and ⊲ represent not being strong and weak overdetermined alternatives:
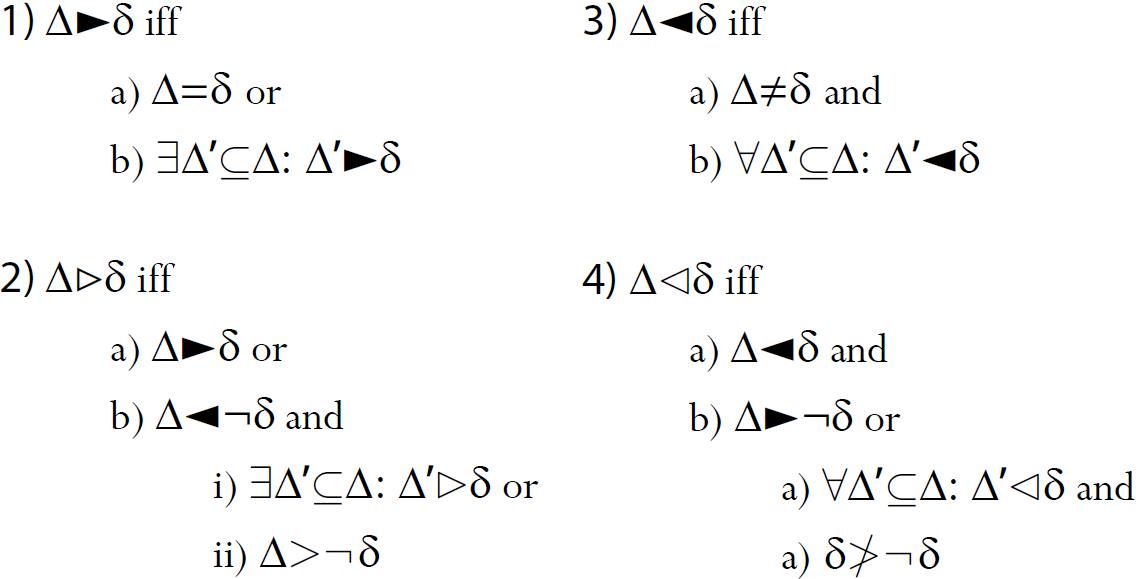
Rule 1 (3) would describe classical diagrammatic systems by defining classic or strong
notions of free ride (δ is a strong free ride from ∆ if and only if δ is the configuration given by ∆ or if there is a subset ∆’
of ∆ from which δ is a strong free ride); while rule 2 (4) would describe non-classical
diagrammatic systems by defining a non-classic or weak notion of free ride (δ is a
weak free ride from ∆ if and only if δ is a strong free ride from ∆ or if ¬δ is not a strong overdetermined
alternative and either for some subset ∆’ of ∆, δ is a weak free ride or δ is preferred
over ¬δ).
With these rules, we can state some relations between classical and non-classical
diagrammatic notions of inference. For example, one plausible but trivial relation
would establish that diagrams obtained by way of strong free rides must also be obtained
by way of weak free rides (but not inversely); and conversely, that weak overdetermined
alternatives must imply not having strong overdetermined alternatives (but not inversely):
❖ Proposition 2
(Subalterns) If ∆►δ, then ∆⊳δ; and if ∆⊲δ, then ∆◄δ.
Another relation would say that strong free rides must not conflict with strong overdetermined
alternatives, and the same for weak free rides and weak overdetermined alternatives:
❖ Proposition 3
(Contradictories) There is no δ s.t. ∆►δ and ∆◄δ, and there is no δ s.t. ∆⊳δ and ∆⊲δ.
Finally, a last couple of relations would establish that strong free rides and weak
overdetermined alternatives must not conflict, but weak free rides and strong overdetermined
alternatives may coexist:
❖ Proposition 4
(Contraries) There is no δ s.t. ∆►δ and ∆⊲δ.
❖ Proposition 5
(Subcontraries) For all δ, ∆⊳δ or ∆◄δ.
These propositions show the coherence of these diagrammatic relations. We can represent
this coherence diagrammatically with the next square of opposition:
Figure 8
A square of opposition
In order to illustrate these relations between classical and nonclassical diagrammatic systems, consider
a couple of examples.
❖ Example 3
Consider an instance of a valid syllogism, say a Barbara syllogism. In Figure 9 we can see Cfg(SAP)≠Cfg(MAPSAM), but for some subset of Cfg(MAPSAM), Cfg(SAP) is indeed a strong free ride, which means that Cfg(SAP) is also a weak free ride (Proposition 2), but it is not a strong nor a weak
overdetermined alternative (Propositions 3 and 4).
Figure 9
MAPSAM►SAP and MAPSAM⊳SAP
❖ Example 4
As a second case, consider an invalid syllogistic form, say MIPSIM∴SIP. Since this
syllogistic form is invalid, it should be the case that its diagrammatic representation
must be an over-determined alternative. Indeed, in Figure 10 we can see that Cfg(SIP)≠Cfg(MIPSIM) and that for all the remaining combinations or subsets of diagrams, Cfg(SIP) is not a strong free ride, which means that Cfg(SIP) is not a strong free ride but a strong overdetermined alternative (Proposition
3), from which it follows that Cfg(SIP) is admissible if regarded as a weak free ride (Proposition 5), but both, ► and
⊳, do not hold (Proposition 4).
Figure 10
MIPSIM►SIP or MIPSIM ⊳ SIP